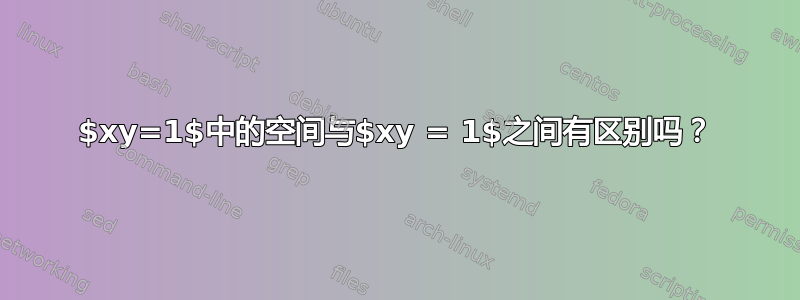
☰

$xy=1$中的空间与$xy = 1$之间有区别吗？

tag-icon • tag-icon math-mode spacing
$xy=1$中的空间与$xy = 1$之间有区别吗？

哪种方法更正确？我没有发现任何差异，但也许我错过了什么？

答案1

没什么区别。让我们看看在编译以下最小示例时如何通过添加\showoutput和检查构造输出：.log

\documentclass{article}
\pagestyle{empty}% To avoid page numbers in the output
\showoutput% Show how the output is constructed
\begin{document}
$xy=1$

$x y = 1$
\end{document}

这是摘录自.log：

Completed box being shipped out [1]
\vbox(633.0+0.0)x407.0
.\glue 16.0
.\vbox(617.0+0.0)x345.0, shifted 62.0
..\vbox(12.0+0.0)x345.0, glue set 12.0fil
...\glue 0.0 plus 1.0fil
...\hbox(0.0+0.0)x345.0
..\glue 25.0
..\glue(\lineskip) 0.0
..\vbox(550.0+0.0)x345.0, glue set 525.99937fil
...\write-{}
...\glue(\topskip) 3.55556
...\hbox(6.44444+1.94444)x345.0, glue set 300.6899fil
....\hbox(0.0+0.0)x15.0
....\mathon                                       <---------------- mathon
....\OML/cmm/m/it/10 x
....\OML/cmm/m/it/10 y
....\kern0.35878
....\glue(\thickmuskip) 2.77771 plus 2.77771
....\OT1/cmr/m/n/10 =
....\penalty 500
....\glue(\thickmuskip) 2.77771 plus 2.77771
....\OT1/cmr/m/n/10 1
....\mathoff                                      <---------------- mathoff
....\penalty 10000
....\glue(\parfillskip) 0.0 plus 1.0fil
....\glue(\rightskip) 0.0
...\glue(\parskip) 0.0 plus 1.0
...\glue(\baselineskip) 3.61111
...\hbox(6.44444+1.94444)x345.0, glue set 300.6899fil
....\hbox(0.0+0.0)x15.0
....\mathon                                       <---------------- mathon
....\OML/cmm/m/it/10 x
....\OML/cmm/m/it/10 y
....\kern0.35878
....\glue(\thickmuskip) 2.77771 plus 2.77771
....\OT1/cmr/m/n/10 =
....\penalty 500
....\glue(\thickmuskip) 2.77771 plus 2.77771
....\OT1/cmr/m/n/10 1
....\mathoff                                      <---------------- mathoff
....\penalty 10000
....\glue(\parfillskip) 0.0 plus 1.0fil
....\glue(\rightskip) 0.0
...\glue 0.0 plus 1.0fil
...\glue 0.0
...\glue 0.0 plus 0.0001fil
..\glue(\baselineskip) 30.0
..\hbox(0.0+0.0)x345.0

我已经强调了上面的重要部分，从调用mathon（处理第一个时调用）开始，到（处理最后一个时调用）$结束：mathoff$

....\mathon                                       <---------------- mathon
....\OML/cmm/m/it/10 x
....\OML/cmm/m/it/10 y
....\kern0.35878
....\glue(\thickmuskip) 2.77771 plus 2.77771
....\OT1/cmr/m/n/10 =
....\penalty 500
....\glue(\thickmuskip) 2.77771 plus 2.77771
....\OT1/cmr/m/n/10 1
....\mathoff                                      <---------------- mathoff

两种情况都是确切地相同，意味着输出是确切地相同。Knuth 也在电子书（第 16 章：输入数学公式，第 127 页）：

不熟悉数学的印刷工排版的公式在数学家看来通常很奇怪，因为新手印刷工通常会把间距弄错。为了缓解这个问题，TeX 在数学公式中自行处理了大部分间距；而且它 忽略您自己在$' 之间添加的任何空格。例如，如果您输入$ x$and $ 2 $，它们的含义与$x$and相同$2$。您可以输入(x + y)/(x - y)or (x+y) / (x-y)，但两者都会导致，即公式中and 符号$(x+y)/(x-y)$周围有一些额外的空格，但 `/ 符号周围没有。因此，您不必记住复杂的数学间距规则，您可以随意使用空格。+-

哪个最好？让你的代码可读，所以在必要时使用空格。

答案2

$xy=1$和$x y = 1$或之间没有区别$ x y = 1 $。它们的渲染结果完全相同：

xy = 1

间距取决于数学原子的分类：

$
\mathord{x}
\mathord{y}
\mathrel{=}
\mathord{1}
$

间距：

  • 公式的开始和结束处没有间距，除了\mathsurround，通常为 0 pt。

  • 普通数学原子之间没有空格（\mathord）。

  • 但是由于\muskip\thickmuskip=的空间\;插入在普通原子和关系（\mathrel）原子之间。

以下示例显示插入的空格：

% plain TeX or LaTeX
\showboxdepth=\maxdimen
\showboxbreadth=\maxdimen
\tracingonline=1
\nonstopmode

\setbox0=\hbox{$x y = 1$}
\showbox0

\csname @@end\endcsname\end % end job for plain TeX and LaTeX

控制台上的结果：

> \box0=
\hbox(6.44444+1.94444)x29.3101
.\mathon
.\teni x
.\teni y
.\kern0.35878
.\glue(\thickmuskip) 2.77771 plus 2.77771
.\tenrm =
.\glue(\thickmuskip) 2.77771 plus 2.77771
.\tenrm 1
.\mathoff

相关内容